Inverse Trig Functions

Just like we did when originally learning about our trig functions, we started our discussion of the inverse trig functions in context of the acute angles and sides of right triangles. Now let's take that a step further and discuss the inverse functions as functions.

You may find it helpful to review of some inverse function properties from precalculus algreba.

Inverse Function Review

Given a function \(f(x)\) and its inverse \(f^{-1}(x)\), the following properties are true.

If \(f\) contains the point \((a,b)\), then \(f^{-1}\) contains the point \((b,a)\).

As an example, the function \(f(x) = x^2\) contains the point \((3,9)\) and its inverse \(f^{-1}(x) = \sqrt{x}\) contains the point \((9,3)\).

The graphs of \(f(x)\) and \(f^{-1}(x)\) are symmetric with respect to the line \(y = x\). This means that they are reflections or mirror images of each other across the diagonal line \(y = x\).
\(f^{-1}(x)\) is only a function if \(f(x)\) is one-to-one. A function is one-to-one if each \(x\)-value corresponds to only one \(y\)-value and each \(y\)-value corresponds to only one \(x\)-value. The first part of this is demonstrated by the vertical line test on \(f(x)\). The second part of this is demonstrated by the horizontal line test on \(f(x)\) or the vertical line test on \(f^{-1}(x)\).

If a function \(f(x)\) is not one-to-one, then \(f^{-1}(x)\) is not a function. However, we can often make it one-to-one by restricting the domain of \(f(x)\) to a smaller part of the whole domain. For example, the graph of \(f(x) = x^2\) over its entire domain \((-\infty, +\infty)\) is not one-to-one because it fails the horizontal line test. This means its inverse would not be a function. However, if we restrict \(f(x) = x^2\) to the part of its domain on\([0, +\infty)\), then it becomes one-to-one and its inverse \(f^{-1}(x) = \sqrt{x}\) is also a function.

This idea is illustrated in the following graphs. In the first graph, we see that the function \(f(x) = x^2\) fails the horizontal line test because there are horizontal lines that cross the graph more than once. The middle graph shows \(f(x) = x^2\) restricted to the domain of \([0, \infty)\) which now passes the horizontal line test. In the third graph, we see that \(f^{-1}(x) = \sqrt{x}\) is a reflection of \(f(x) = x^2\) across the \(y = x\) line.

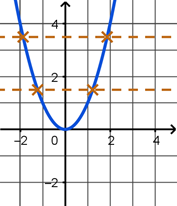
Graph of y equals x squared with two horizontal lines that each cross the curve twice.

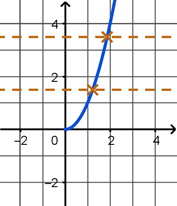
Part of the graph of y equals x squared for x greater than or equal to 0 with two horizontal lines that each cross the curve once.

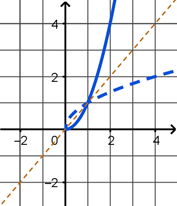
Graph of y equals x square restricted to the interval from 0 to infinity, the line y equals x, and the graph of y equals the square root of x.

The domain and range of \(f(x)\) flip and become the range and domain of \(f^{-1}(x)\), respectively.

Using the same example of \(f(x) = x^2\) and \(f^{-1}(x) = \sqrt{x}\), the restricted domain of \(f\) is \([0, \infty)\) which is the range of \(f^{-1}\). Similarly, the restricted range of \(f\) is \([0, \infty)\) which is the domain of \(f^{-1}\)

The compositions of \(f(x)\) with \(f^{-1}(x)\) should cancel out. In other words, a function and its inverse must satisfy the equations \(f\left(f^{-1}(x)\right) = x\) and \(f^{-1}\left(f(x)\right) = x\).

Continuing with our example of \(f(x) = x^2\) and \(f^{-1}(x) = \sqrt{x}\), we get the following compositions.

\[f\left(f^{-1}(x)\right) = \left(\sqrt{x}\right)^2 = x\] \[f^{-1}\left(f(x)\right) = \sqrt{x^2} = x\]

We see that both compositions cancel out. The input of the composition expression, \(x\), equals the output of the composition expression, \(x\).

The following table gives the restricted domain graph for the 3 main trig functions, the corresponding inverse trig function graph, the domain and range of the inverse trig function, and the part of the unit circle that corresponds to the range for the inverse trig functions. Note that while it is possible to think of these inverse functions in terms of degree units, we want to default to thinking in terms of radian values. Let the context of a problem determine whether to work in degrees or radians.

Inverse Trig and the Unit Circle

Restricted

Inverse

Domain and Range

Unit Circle

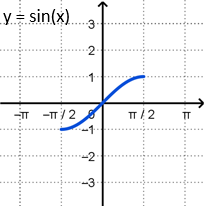
Graph of y equals sine of x on a restricted domain from negative pi over 2 to pi over 2.

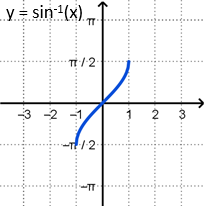
Graph of y equals the inverse sine of x.

The inverse function \(y = \sin^{-1}{x}\) is restricted to the following domain and range.

Domain: \([-1,1]\)
Range: \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\)

This range corresponds to angle values on the right half of the unit circle.

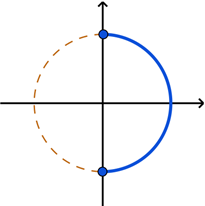
Graph of the unit circle with the right half highlighted, from negative pi over 2 to pi over 2.

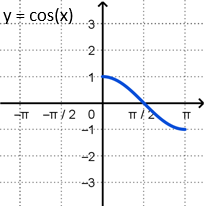
Graph of y equals cosine of x on a restricted domain from 0 to pi.

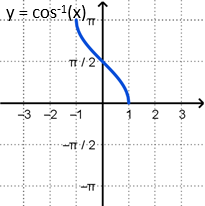
Graph of y equals the inverse cosine of x.

The inverse function \(y = \cos^{-1}{x}\) is restricted to the following domain and range.

Domain: \([-1,1]\)
Range: \([0,\pi]\)

This range corresponds to angle values on the top half of the unit circle.

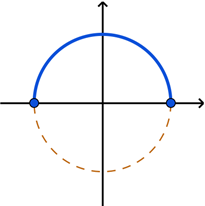
Graph of the unit circle with the top half highlighted, from 0 to pi.

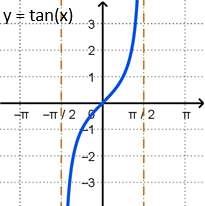
Graph of y equals tanget of x on a restricted domain from negative pi over 2 to pi over 2.

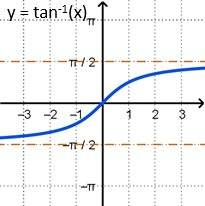
Graph of y equals the inverse tangent of x.

The inverse function \(y = \tan^{-1}{x}\) is restricted to the following domain and range.

Domain: \((-\infty,\infty)\)
Range: \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\)

This range corresponds to angle values on the right half of the unit circle, excluding the points on the \(y\)-axis.

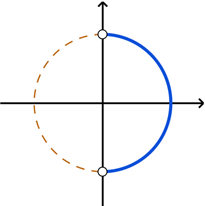
Remember that since the inverse trig functions are functions, there can be only a single answer for any inverse trig expression. It is possible to be undefined too. Let's work through some examples of computing inverse trig values.

Self-Check #4: Evaluate the expression \(\sin^{-1}\left(-\frac{1}{2}\right)\). (Select the most appropriate response.)

(A) \(-\frac{\pi}{6}\) (B) \(\frac{\pi}{6}\) (C) \(\frac{5\pi}{6}\) (D) Undefined

You must select an answer above.

(Answer: A) -- The expression \(\sin^{-1}\left(-\frac{1}{2}\right)\) must result in an angle within the range of \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\), which corresponds to the right half of the unit circle. In particular, it is the angle \(\theta\) where \(\sin(\theta) = -\frac{1}{2}\). Even though \(\sin\left(\frac{5\pi}{6}\right) = -\frac{1}{2}\), the angle \(\frac{5\pi}{6}\) is not within the range and can be ignored. Since we know \(\sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\) and that sine is negative in the 4^th quadrant, we can conclude that \(\sin^{-1}\left(-\frac{1}{2}\right) = -\frac{\pi}{6}\).

Self-Check #6: Evaluate the expression \(\tan^{-1}(-1)\). (Select the most appropriate response.)

(A) \(\frac{5\pi}{4}\) (B) \(\pi\) (C) \(-\frac{\pi}{4}\) (D) Undefined

You must select an answer above.

(Answer: C) -- The expression \(\tan^{-1}(-1)\) must result in an angle within the range of \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\), which corresponds to the right half of the unit circle. In particular, it is the angle \(\theta\) where \(\tan(\theta) = -1\). From the unit circle, we know that both \(\tan\left(-\frac{\pi}{4}\right) = -1\) and \(\tan\left(\frac{5\pi}{4}\right) = -1\). We also know that \(-\frac{\pi}{4}\) and \(\frac{5\pi}{4}\) are in the 4^th quadrant. In fact, these two angles are coterminal to each other. But the angle \(\frac{5\pi}{4}\) is not within the range and can be ignored. Thus, we can conclude that \(\tan^{-1}(-1) = -\frac{\pi}{4}\).