Shifted Parabolas

Now that we have seen the standard conic form of a parabola having a vertex at the origin, we next want to consider how we can work with a parabola that is not located at the origin. Recall that a function with a horizontal shift will have the general factor expression \((x-h)\). So for example, the expression \((x-3)\) represents a shift of 3 units in the positive \(x\)-direction while the expression \((x+1)\) is a shift of 1 unit in the negative \(x\)-direction. We can apply the same idea to vertical shifts, \((y-k)\). So, \((y-2)\) is a vertical shift of 2 units in the positive \(y\)-direction while \((y+5)\) is a vertical shift of 5 units in the negative \(y\)-direction. Let's look at the standard formula, the key characteristics, and then a few examples of shifted parabolas.

The standard conic equations of a parabola with vertex at the point \((h,k)\) have the following form.

Vertical Axis of Symmetry

Horizontal Axis of Symmetry

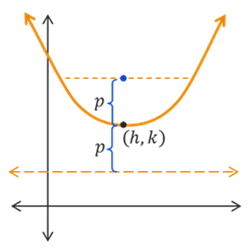\[(x-h)^2 = 4p(y-k)\]

The focus is located at the point \((h,p+k)\) and the directrix is the horizontal line \(y = -p+k\). The parabola will open up if \(p > 0\) or down if \(p < 0\). The focal diameter length is \(|4p|\).

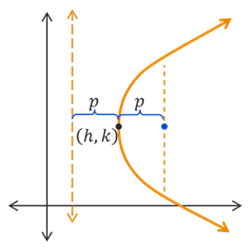Graph of a parabola opening to the right with a horizontal axis of symmetry passing through the vertex, which is located at the point (h,k). The focus point is located on the axis of symmetry inside the curvature of the parabola and the vertical directrix is located to the left of the parabola. The distance between the focus and vertex and between the directrix and vertex are both labeled as p. The width of the parabola is measured by the focal diameter, which is parallel to the directrix and extends from one side of the parabola to the other side while passing through the focus.

\[(y-k)^2 = 4p(x-h)\]

The focus is located at the point \((p+h,k)\) and the directrix is the vertical line \(x = -p+h\). The parabola will open right if \(p > 0\) or left if \(p < 0\). The focal diameter length is \(|4p|\).

When dealing with shifted parabolas, the overall shape and distances remain the same. That means that \(p\) still gives us the distance from the vertex to the focus and the distance from the vertex to the directrix. The parabola still curves around the focus and away from the directrix. The length of the focal diameter is still \(|4p|\). The only thing that has changed is that the location of everything has been shifted horizontally by \(h\) and vertically by \(k\).

Let's look at some examples of parabolas that have been shifted away from the origin.