
Angle Measure
Trigonometric Functions

Trigonometric Functions
Since angles can be defined as unlimited rotation, the terminal side of an angle will repeat its path as it completes full revoluions about its vertex. When that happens, these two angles are said to be coterminal.
Two angles in standard position are coterminal if their terminal sides are at the same position, regardless of the amount or direction of rotation. In addition, any angle whose terminal side is located on the \(x\) or \(y\) axis is called a quadrantal angle.
The three graphs below are all coterminal to each other. Each angle is given in both radians and degrees so that you can see how they are related to each other using both units.
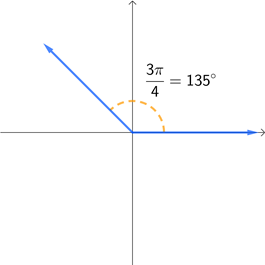
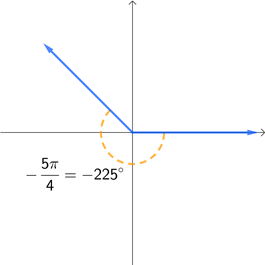
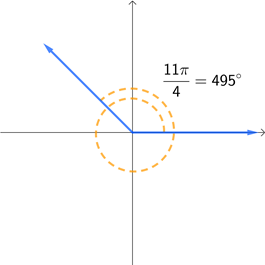
How can we show that 135°, -225°, and 495° are all coterminal with each other? Or similarly, how can we show that \(\frac{3\pi}{4}\), \(-\frac{5\pi}{4}\), and \(\frac{11\pi}{4}\) are all coterminal with each other? We already know that they all have the same terminal side, so how can we verify this algebraically?
Let's start by showing that the angles in degrees are each 360° apart from each other. There are several ways to do this, but for now let's just subtract each pair of angles, subtracting the larger value minus the smaller value.
\[\begin{align*} 135^{\circ} - \left(-225^{\circ}\right) &= \color{red}360^{\circ}\color{black} \\ 495^{\circ} - 135^{\circ} &= \color{red}360^{\circ}\color{black} \\ 495^{\circ} - \left(-225^{\circ}\right) &= 720^{\circ} = 2 \cdot \color{red}360^{\circ}\color{black} \end{align*}\]Notice that the difference between each pairing of angles is 360° or a multiple of 360°. This means they are coterminal to each other, which should make sense because they all share the same location for their terminal side. Let's repeat this process for the angles given in radians.
\[\begin{align*} \frac{3\pi}{4} - \left(-\frac{5\pi}{4}\right) = \frac{3\pi+5\pi}{4} = \frac{8\pi}{4} &= \color{red}2\pi\color{black} \\ \frac{11\pi}{4} - \frac{3\pi}{4} = \frac{11\pi-3\pi}{4} = \frac{8\pi}{4} &= \color{red}2\pi\color{black} \\ \frac{11\pi}{4} - \left(-\frac{5\pi}{4}\right) = \frac{11\pi+5\pi}{4} = \frac{16\pi}{4} &= 4\pi = 2 \cdot \color{red}2\pi\color{black} \end{align*}\]Again, we see that the difference between each pair of angles is \(2\pi\) or a multiple of \(2\pi\). These results confirm that the given angle measures, whether given in degrees or radians, are coterminal.
The following video gives a few examples of how we can find a coterminal angle on a specific interval for any given angle.
Self-Check #3: Find an angle on the interval \([0, 2\pi)\) that is coterminal to \(\frac{36\pi}{7}\). (Select the most appropriate response.)
(Answer: B) -- First, rewrite \(2\pi\) with a common denominator of 7, which is \(2\pi = \frac{2\pi \cdot 7}{1 \cdot 7} = \frac{14\pi}{7}\). Since the given angle \(\frac{36\pi}{7}\) is greater that \(\frac{14\pi}{7}\), we need to subtract \(2\pi\), and we will repeatedly do so until we get a value that is less than \(\frac{14\pi}{7}\), or \(2\pi\).
\[\frac{36\pi}{7} - 2\pi = \frac{36\pi}{7} - \frac{14\pi}{7} = \frac{36\pi-14\pi}{7} = \frac{22\pi}{7}\]But this is not less than \(\frac{14\pi}{7}\), so we need to subtract \(2\pi\) again.
\[\frac{22\pi}{7} - 2\pi = \frac{22\pi}{7} - \frac{14\pi}{7} = \frac{22\pi-14\pi}{7} = \frac{8\pi}{7}\]Since this value is less than \(\frac{14\pi}{7}\), we now know that the angle on \([0, 2\pi)\) that is coterminal to \(\frac{36\pi}{7}\) is \(\frac{8\pi}{7}\).