Angle Measure

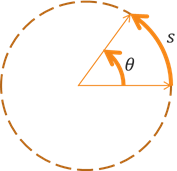
Linear speed is the rate at which an object travels along the arc of a circle and is measured in units of length per unit of time. Given a distance of \(s\) along a circular arc travelled over time \(t\), the linear speed \(v\) is given by the following formula.

\[v = \frac{s}{t}\]

Angular speed is the rate at which an object rotates about its vertex and is measured in radians per unit of time. Given a rotation of \(\theta\) radians over time \(t\), the angular speed \(\omega\) is given by the following formula, where \(\omega\) is the Greek letter "omega."

\[\omega = \frac{\theta}{t}\]

For a circle of radius \(r\), the linear and angular speeds are related by \(v = \omega r\).