Graphing Trig Functions

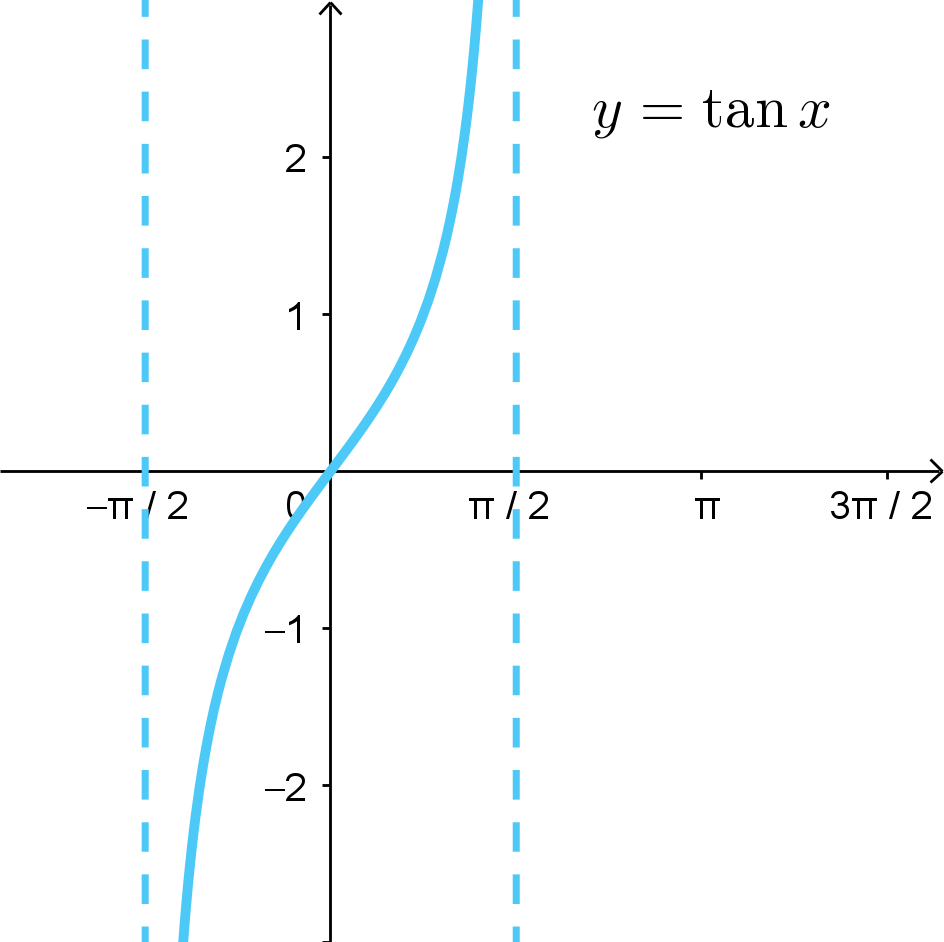
The period length of \(y = \tan{x}\) is \(\pi\). The base 1-period portion of the graph is over the interval \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\). It will repeat forever as \(x \rightarrow -\infty\) and \(x \rightarrow +\infty\).

The domain of \(y = \tan{x}\) is all Real numbers except odd integer multiples of \(\frac{\pi}{2}\), which result in vertical asymptotes. So, there are vertical asymptoes at \(... -\frac{5\pi}{2}, -\frac{3\pi}{2}, -\frac{\pi}{2}, \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, ...\). The range of \(y = \tan{x}\) is \((-\infty, +\infty)\).

Note that \(y = \tan{x}\) is always a increasing function.

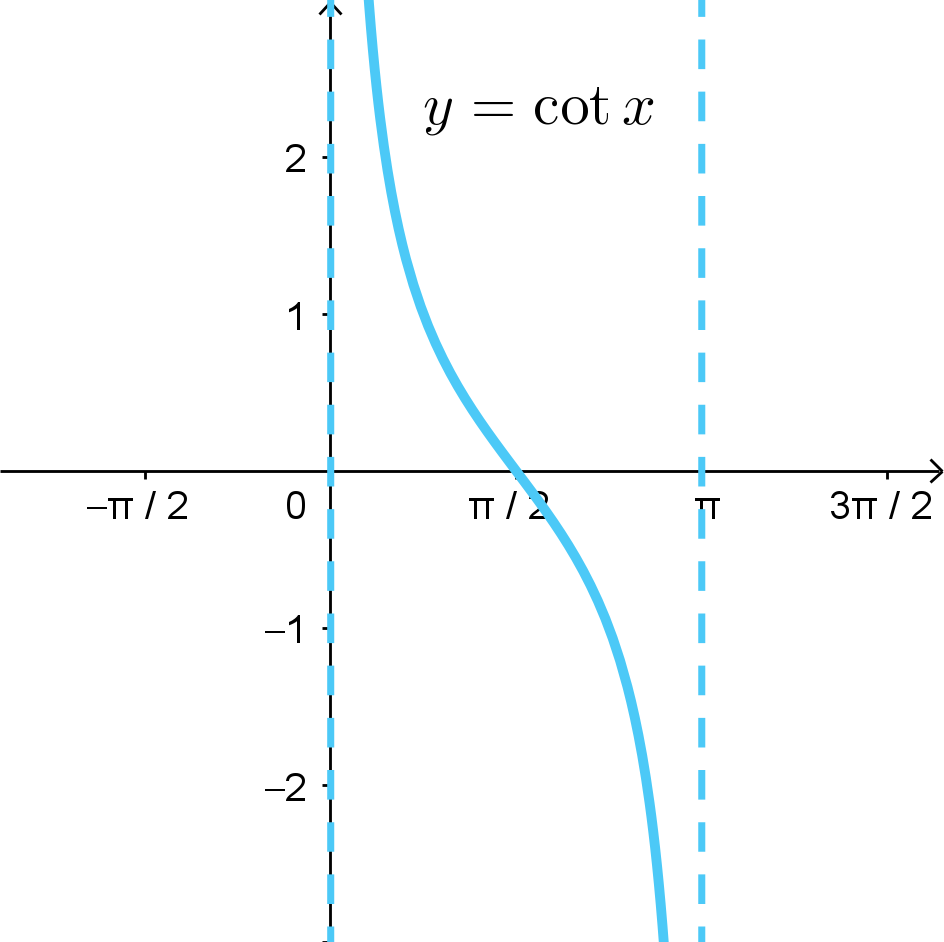
The period length of \(y = \cot{x}\) is \(\pi\). The base 1-period portion of the graph is over the interval \((0,\pi)\). It will repeat forever as \(x \rightarrow -\infty\) and \(x \rightarrow +\infty\).

The domain of \(y = \cot{x}\) is all Real numbers except integer multiples of \(\pi\), which result in vertical asymptotes. So, there are vertical asymptoes at \(... -3\pi, -2\pi, -\pi, 0, \pi, 2\pi, 3\pi, ...\). The range of \(y = \cot{x}\) is \((-\infty, +\infty)\).

Note that \(y = \cot{x}\) is always a decreasing function.

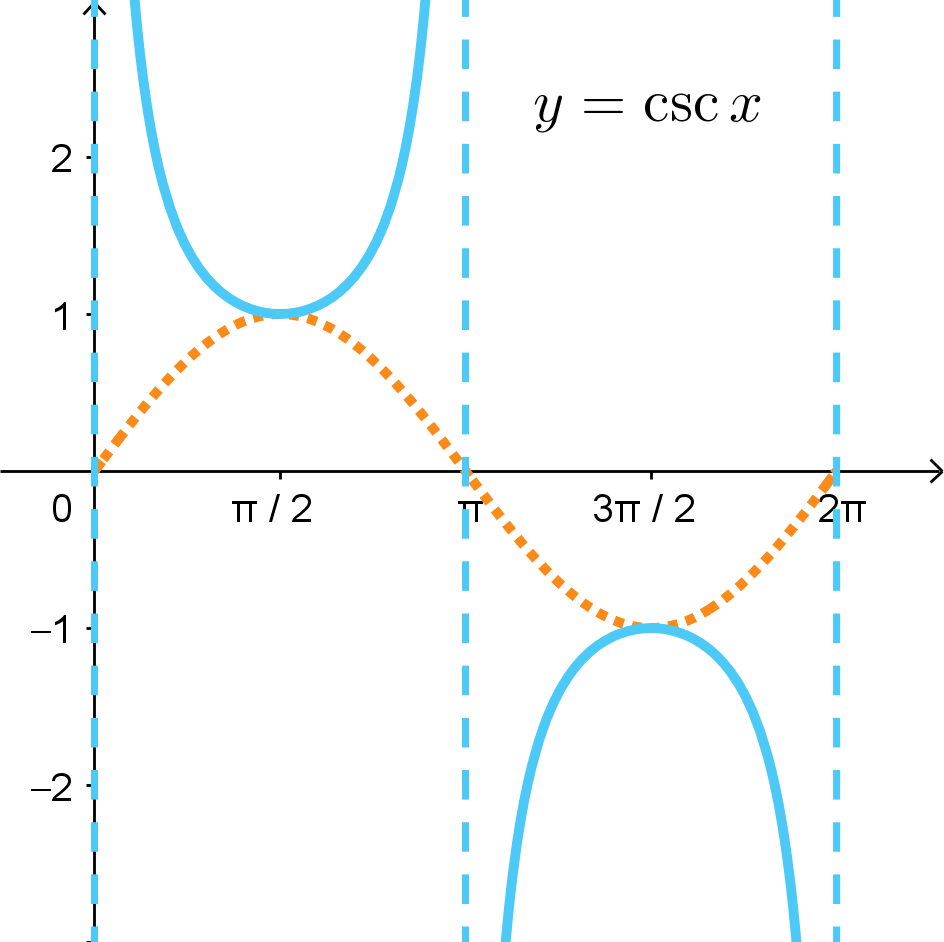
The period length of \(y = \csc{x}\) is \(2\pi\). The base 1-period portion of the graph is over the interval \((0,2\pi)\). It will repeat forever as \(x \rightarrow -\infty\) and \(x \rightarrow +\infty\).

The domain of \(y = \csc{x}\) is all Real numbers except integer multiples of \(\pi\), which result in vertical asymptotes. So, there are vertical asymptoes at \(... -3\pi, -2\pi, -\pi, 0, \pi, 2\pi, 3\pi, ...\). The range of \(y = \csc{x}\) is \((-\infty,-1) \cup (1,+\infty)\).

One way to remember the graph of \(y = \csc{x}\) is to picture it as a reflection of \(y = \sin{x}\) away from the \(x\)-axis, and it will have vertical asymptotes wherever \(y = \sin{x}\) cross the \(x\)-axis. This is because cosecant and sine are reciprocals of each other.

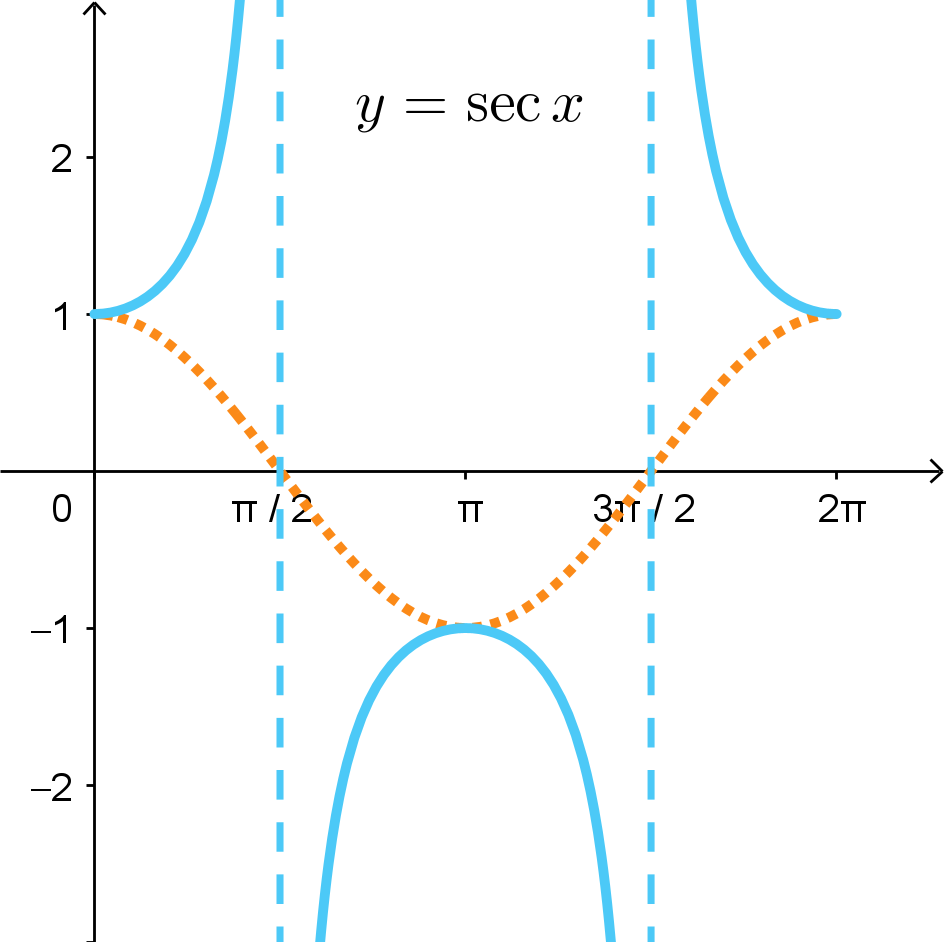
The period length of \(y = \sec{x}\) is \(2\pi\). The base 1-period portion of the graph is over the interval \([0,2\pi]\). It will repeat forever as \(x \rightarrow -\infty\) and \(x \rightarrow +\infty\).

The domain of \(y = \sec{x}\) is all Real numbers except odd integer multiples of \(\frac{\pi}{2}\), which result in vertical asymptotes. So, there are vertical asymptoes at \(... -\frac{5\pi}{2}, -\frac{3\pi}{2}, -\frac{\pi}{2}, \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, ...\). The range of \(y = \sec{x}\) is \((-\infty,-1) \cup (1,+\infty)\).

One way to remember the graph of \(y = \sec{x}\) is to picture it as a reflection of \(y = \cos{x}\) away from the \(x\)-axis, and it will have vertical asymptotes wherever \(y = \cos{x}\) cross the \(x\)-axis. This is because secant and cosine are reciprocals of each other.