Vectors

Vector Applications

Application problems involving vectors will often express the direction in different ways. For example, we could describe the direction of a vector using an angle in standard position, so \(\theta = 0^{\circ}\) corresponds to due east (the positive \(x\)-axis) and counterclockwise rotation is positive. Using a compass, \(\theta = 0^{\circ}\) corresponds to due north (the positive \(y\)-axis) and positive rotation is clockwise for \(0^{\circ} \le \theta \lt 360^{\circ}\).

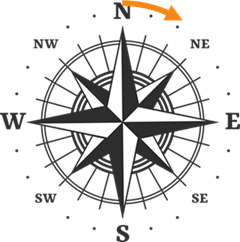
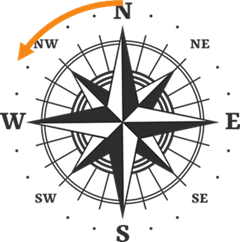
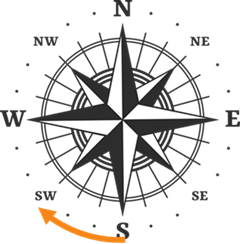
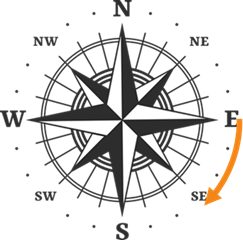
Another method that we will use to describe headings or bearings is to use a mix of the cardinal directions N, S, E, and W. By pairing two cardinal directions together along with an acute angle, we can describe any directionl in any quadrant. In each example below, note that the first letter tells us the cardinal direction where the angle starts rotating and the second letter tells us which direction it rotates towards. So, a \(N30^{\circ}E\) heading starts in the due north direction and rotates \(30^{\circ}\) towards the east. This would correspond to a \(60^{\circ}\) standard position angle.

Applications using vectors will typically involve expressing vector quantities in component form, performing vector operations, and then finding the magnitude and direction of a vector. Let's look at a couple examples.