Vector Operations

Operations involving Real numbers, or scalars, involve how we add or subtract, multiply or divide, or use powers or exponents. When looking at vector operations, we need to distinguish between scalar and vector operations. The most common are vector additiona, vector subtraction, and scalar multiplication of a vector. Let's define the process and then look at how they work.

Suppose \(\textbf{u} = \left< a,b \right>\) and \(\textbf{v}= \left< c,d \right> \) are vectors and \(k\) is a scalar.

Vector Addition: \(\,\qquad \textbf{u} + \textbf{v} = \left< a,b \right> + \left< c,d \right> = \left< a+c, b+d \right>\)
Vector Subtraction: \(\quad \textbf{u} - \textbf{v} = \left< a,b \right> - \left< c,d \right> = \left< a-c, b-d \right>\)
Scalar Multiplication: \(\,\, k\textbf{u} = k\left< a,b \right> = \left< ka, kb \right>\)

What these formulas tell us is that when adding or subtracting two vectors, we can just add or subtract the corresponding components. Similarly, when multiplying a vector by a scalar, we can just distribute the scalar to each component of the vector.

Let's look at some examples of these vector operations, including with a more graphical perspective.

Unit Vectors

A special type of vector, called a unit vector, is a vector whose length, or magnitude, is 1. In other words, a vector \(\textbf{v}\) is a unit vector if \(|\textbf{v}| = 1\). Sometimes you may see unit vectors expressed with a "hat" symbol rather than an arrow, such as \(\hat{v}\) instead of \(\vec{v}\).

Two unique unit vectors are \(\textbf{i} = \hat{\imath} = \left< 1,0 \right>\) and \(\textbf{j} = \hat{\jmath} = \left< 0,1 \right>\).

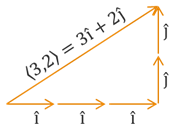
These \(\textbf{ij}\) unit vectors can be used to describe the components of a given vector. In the following illustration, we see that vector \(\left< 3,2 \right>\) and be expressed as the sum of 3 \(\textbf{i}\) vectors with 2 \(\textbf{j}\) vectors. Graph of vector <3,2> that is corresponds to the sum of 3 i-vectors followed by 2 j-vectors.

Graph of vector <3,2> that is corresponds to the sum of 3 i-vectors followed by 2 j-vectors.

By applying vector operations, we can expression any vector in either its component form or \(\textbf{ij}\) form. In other words, \(\textbf{v} = \left< a,b \right> = a\textbf{i} + b\textbf{j}\).